Building Thinking Classrooms in Mathematics: A Comprehensive Plan
Peter Liljedahl’s work, including resources like the “Building Thinking Classrooms in Mathematics” PDF, offers a transformative approach to math education, focusing on student thinking.
DoDEA’s professional development and the Mississippi State partnership exemplify the growing adoption of these innovative strategies for enhanced learning outcomes.
Building Thinking Classrooms (BTC) represents a paradigm shift in mathematics education, moving away from traditional, teacher-centered approaches towards student-driven exploration and problem-solving. Peter Liljedahl’s framework, detailed in resources like the “Building Thinking Classrooms in Mathematics” PDF, emphasizes the importance of fostering a classroom environment where thinking is visible and valued.
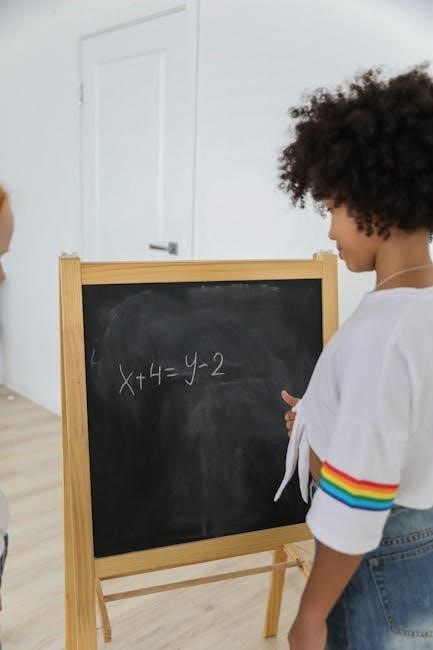
This approach challenges conventional methods by prioritizing rich, open-ended tasks that allow for multiple entry points and solution pathways. The core idea revolves around creating conditions that encourage students to actively engage with mathematical concepts, collaborate with peers, and develop a deeper conceptual understanding. DoDEA’s implementation and the Mississippi State partnership demonstrate a commitment to this innovative pedagogy, aiming to improve math achievement and reduce math anxiety.
Peter Liljedahl’s Core Principles
Peter Liljedahl’s core principles, thoroughly outlined in the “Building Thinking Classrooms in Mathematics” PDF, center on transforming the learning environment to prioritize student thinking. He advocates for tasks that are low-floor, high-ceiling, accessible to all learners yet offering opportunities for advanced exploration.
Central to his philosophy is the idea of “sweet spot” tasks – challenging enough to promote cognitive effort, but not so difficult as to induce frustration. Liljedahl stresses the importance of vertical non-permanent surfaces (VNPS) to make thinking visible and facilitate collaboration. These principles, actively implemented by DoDEA and the Mississippi State partnership, aim to cultivate a classroom culture where mathematical reasoning and problem-solving are paramount.
The Five Essential Conditions
The “Building Thinking Classrooms in Mathematics” PDF details five essential conditions for successful implementation. These include utilizing low-floor, high-ceiling tasks, ensuring tasks reside within the “sweet spot” for optimal challenge, and employing vertical non-permanent surfaces (VNPS) for visible thinking.
Furthermore, Liljedahl emphasizes the importance of structuring tasks to allow for multiple entry points and encouraging students to collaborate and share their reasoning. Finally, the fifth condition centers on the teacher’s role shifting from “teller” to “facilitator,” fostering a classroom environment where student thinking takes center stage, as demonstrated in programs like DoDEA’s training.

Low-Floor, High-Ceiling Tasks
As outlined in the “Building Thinking Classrooms in Mathematics” PDF, low-floor, high-ceiling tasks are central to fostering equitable access and maximizing student engagement. These tasks possess a simple starting point – the “low floor” – allowing all students to immediately engage with the material.

Simultaneously, they offer opportunities for increasingly complex exploration and problem-solving – the “high ceiling” – challenging advanced learners. This design ensures that every student can experience success and be appropriately challenged, promoting a growth mindset and deeper understanding of mathematical concepts, a key focus of the DoDEA program.
Sweet Spot Tasks
The “Building Thinking Classrooms in Mathematics” PDF emphasizes the importance of “sweet spot” tasks, building upon the foundation of low-floor, high-ceiling designs. These tasks reside within the zone of proximal development, offering a level of challenge that is neither too easy nor too difficult for the majority of students.

Sweet spot tasks encourage productive struggle, prompting students to actively construct their understanding through exploration and collaboration. They are intentionally designed to reveal student thinking, allowing teachers to provide targeted support and facilitate meaningful mathematical discourse, aligning with the goals of the Mississippi State partnership program.
Vertical Non-Permanent Surfaces
The “Building Thinking Classrooms in Mathematics” PDF champions the use of Vertical Non-Permanent Surfaces (VNPS), like whiteboards, as central tools for fostering student thinking. These surfaces provide a dedicated space for students to externalize their mathematical ideas, making their thought processes visible to themselves and their peers.
VNPS facilitate collaboration and communication, enabling students to build upon each other’s work and engage in productive mathematical discussions. DoDEA’s implementation highlights how these surfaces transform classrooms into dynamic learning environments, supporting the core principles of Peter Liljedahl’s approach and promoting deeper understanding.
Task Design and Implementation
The “Building Thinking Classrooms in Mathematics” PDF emphasizes careful task design as crucial for successful implementation. Tasks should be “low-floor, high-ceiling,” accessible to all students yet offering opportunities for extension and challenge. Effective tasks encourage multiple entry points and diverse solution strategies, promoting equitable participation.
The teacher’s role shifts from direct instruction to facilitator, observing student thinking and providing targeted support. DoDEA’s professional development focuses on equipping educators with the skills to design and implement these tasks effectively, fostering a classroom culture where thinking is valued and nurtured.
Designing Effective Low-Floor, High-Ceiling Tasks
The “Building Thinking Classrooms in Mathematics” PDF details how to craft tasks accessible to all learners, regardless of prior knowledge – the “low-floor” aspect. Simultaneously, these tasks must offer significant challenge and extension possibilities, the “high-ceiling.” This is achieved through open-ended questions and multiple solution pathways.

Effective tasks avoid specific procedures, instead prompting students to explore, conjecture, and justify their reasoning. The goal isn’t necessarily the correct answer, but the thinking process itself. Careful consideration of potential student approaches is vital during task design, ensuring equitable access and maximizing cognitive demand.
The Role of the Teacher in a Thinking Classroom
The “Building Thinking Classrooms in Mathematics” PDF emphasizes a significant shift in the teacher’s role. Instead of being the primary deliverer of information, the teacher becomes a facilitator of thinking. This involves carefully launching tasks, then strategically circulating to observe student approaches without intervention, initially;
Effective questioning is crucial – probing student thinking, asking for justifications, and encouraging peer-to-peer interaction. The teacher synthesizes observed thinking during whole-class discussions, highlighting different strategies and misconceptions. This approach fosters a culture of intellectual risk-taking and deepens understanding.
Vertical Non-Permanent Surfaces: Benefits and Practicalities

“Building Thinking Classrooms in Mathematics” highlights Vertical Non-Permanent Surfaces (VNPS) – like whiteboards – as essential tools. These surfaces allow all students to simultaneously externalize their thinking, making it visible to themselves and peers. This contrasts with traditional methods where only a few students share work publicly.

VNPS promote collaboration, as students readily build upon each other’s ideas. They also offer a low-stakes environment for experimentation and revision. Practical considerations include ensuring sufficient surface area and providing appropriate markers. The PDF details how VNPS fundamentally change classroom dynamics, fostering a more active and engaging learning experience.
Whiteboards as Thinking Tools
“Building Thinking Classrooms in Mathematics” emphasizes that whiteboards aren’t merely for displaying answers; they are powerful cognitive tools. The PDF details how students utilize these surfaces to sketch diagrams, write equations, and represent their mathematical reasoning. This externalization of thought processes is crucial for both individual understanding and collaborative problem-solving.
Whiteboards facilitate iterative thinking, allowing students to easily modify and refine their approaches. They also provide a shared space for collective brainstorming and knowledge construction. The book stresses that the process visible on the whiteboard is more valuable than the final product.
Student Interaction and Collaboration with VNPS
“Building Thinking Classrooms in Mathematics”, as detailed in the PDF, highlights how Vertical Non-Permanent Surfaces (VNPS) fundamentally alter student interaction. Students move freely, observing peers’ work, offering suggestions, and challenging assumptions. This dynamic environment fosters a collaborative learning culture, shifting away from isolated individual work.
The VNPS encourages “productive struggle” as students learn from each other’s mistakes and diverse approaches. The PDF emphasizes that the teacher’s role shifts from lecturer to facilitator, guiding discussions and prompting deeper thinking. This collaborative process builds confidence and a stronger conceptual understanding of mathematical concepts.
The Importance of Formative Assessment

“Building Thinking Classrooms in Mathematics”, outlined in the PDF, stresses that formative assessment isn’t about grading, but understanding student thinking. Observing students at work on VNPS allows teachers to identify misconceptions and adjust instruction in real-time. The PDF details how to interpret student work, looking beyond correct answers to assess their reasoning and problem-solving strategies.
This observational data informs subsequent task design and targeted interventions. Effective formative assessment, as Liljedahl advocates, moves away from traditional testing and towards a continuous cycle of observation, interpretation, and instructional refinement, ultimately fostering deeper mathematical understanding.
Observing and Interpreting Student Thinking
The “Building Thinking Classrooms in Mathematics” PDF emphasizes shifting from “checking for answers” to actively observing how students are thinking. Teachers should circulate during tasks, listening to discussions and noting strategies employed on Vertical Non-Permanent Surfaces (VNPS). Interpretation goes beyond correctness; look for partial understandings, common errors, and unique approaches.
Liljedahl’s approach encourages teachers to ask clarifying questions – “Tell me more about why you did that?” – rather than providing solutions. This reveals the student’s thought process. Documenting these observations, even briefly, provides valuable data for informing future instruction and task selection.
Using Assessment to Inform Instruction
The “Building Thinking Classrooms in Mathematics” PDF advocates for formative assessment as a continuous cycle, driven by observations of student thinking. Instead of solely relying on summative tests, teachers use insights gained from observing VNPS work to adjust future tasks and instructional approaches.
If many students struggle with a specific concept, the teacher might modify the task’s “sweet spot” or provide targeted support. This isn’t about “re-teaching” but about providing opportunities for students to grapple with the idea in new ways. Assessment informs what is taught next, not just if it was learned.
Modifying Thinking Classrooms for Different Settings
The “Building Thinking Classrooms in Mathematics” PDF acknowledges that a one-size-fits-all approach isn’t feasible. Liljedahl’s supplemental title, “Modifying Your Thinking Classroom for Different Settings,” directly addresses adapting the core principles to diverse environments.
Challenges like limited space or varying student needs require creative solutions. This might involve utilizing smaller VNPS, incorporating digital tools, or adjusting task complexity. The key is maintaining the five essential conditions – even in non-traditional classrooms. Successful implementation necessitates flexibility and a commitment to prioritizing student thinking above rigid adherence to a specific model.
Adapting to Diverse Classroom Environments
The “Building Thinking Classrooms in Mathematics” PDF highlights the necessity of tailoring implementation to unique contexts. Diverse classrooms present varied challenges – from physical space limitations to differing student backgrounds and learning styles.
Adapting might involve utilizing mobile VNPS, leveraging technology for task presentation, or modifying tasks to be culturally relevant. Consider grouping strategies that promote equitable participation. The core principles remain constant, but the how must be flexible. Successful adaptation requires ongoing observation, reflection, and a willingness to experiment with different approaches to ensure all students can engage in rich mathematical thinking.
Addressing Challenges in Implementation
The “Building Thinking Classrooms in Mathematics” PDF acknowledges that shifting to this pedagogical approach isn’t without hurdles. Common challenges include teacher discomfort with relinquishing control, student resistance to increased cognitive demand, and logistical issues with VNPS.
Overcoming these requires sustained professional development, collaborative planning, and a focus on small, incremental changes. Addressing math anxiety is crucial, as is clearly communicating expectations. The PDF emphasizes the importance of observing student thinking to inform adjustments. Patience and persistence are key; building a thinking classroom is a process, not an event, demanding ongoing refinement.

Building Thinking Classrooms in Mathematics: Grades K-12 ― Book Overview
Peter Liljedahl’s “Building Thinking Classrooms in Mathematics: Grades K-12”, available as a PDF and in print, details a comprehensive framework for transforming math instruction. The book outlines five essential conditions – launching tasks, fostering sweet spots, utilizing VNPS, and emphasizing formative assessment – to cultivate student thinking.
It provides practical guidance on task design, teacher roles, and adapting the approach across grade levels. A supplemental title, “Modifying Your Thinking Classroom for Different Settings”, further expands on implementation strategies. The book is a cornerstone resource for educators seeking to move beyond traditional methods.
Professional Development and Training
DoDEA (Department of Defense Education Activity) Americas Secondary Math ISS Team recently completed a significant professional development course centered around “Building Thinking Classrooms”, utilizing the PDF resource and related materials. This training involved 114 pre-K through 12th-grade educators, demonstrating a widespread commitment to this pedagogical shift.
Furthermore, a partnership between Mississippi State and Starkville Oktibbeha Consolidated School Districts is actively engaging educators in professional development focused on implementing these strategies. These initiatives highlight the growing demand for training and support in adopting Liljedahl’s methods.
DoDEA’s Implementation of Building Thinking Classrooms
DoDEA’s Americas Secondary Math ISS Team spearheaded a groundbreaking professional development initiative focused on “Building Thinking Classrooms”, leveraging the comprehensive PDF resource. This intensive course brought together 114 educators spanning pre-kindergarten through 12th grade, showcasing a broad organizational commitment to transforming math instruction.
The program aimed to equip teachers with the tools and understanding necessary to implement Peter Liljedahl’s core principles, fostering a learning environment that prioritizes student thinking and problem-solving. This initiative represents a significant investment in improving math education within the DoDEA system.
Mississippi State & Starkville Oktibbeha Partnership Program
A collaborative effort between Mississippi State University and the Starkville Oktibbeha Consolidated School Districts is actively engaging both aspiring and current secondary math educators. This partnership centers around the implementation of strategies detailed in resources like the “Building Thinking Classrooms in Mathematics” PDF, promoting innovative teaching practices.
The program focuses on equipping teachers with the skills to create dynamic learning environments where students are encouraged to think critically and collaboratively. This initiative demonstrates a commitment to enhancing math education within the local community, utilizing Liljedahl’s methods.
Addressing Math Anxiety and Building Confidence
Building Thinking Classrooms, as outlined in resources like the “Building Thinking Classrooms in Mathematics” PDF, inherently addresses math anxiety by shifting the focus from correct answers to the thinking process itself. The low-floor, high-ceiling tasks and collaborative environment reduce pressure and foster a growth mindset.
By emphasizing exploration and shared reasoning, students gain confidence in their abilities, even when facing challenging problems. This approach acknowledges that struggle is a natural part of learning, creating a safe space for risk-taking and ultimately diminishing anxiety surrounding mathematics.
The Connection to Mathematical Practices
Building Thinking Classrooms, detailed in the “Building Thinking Classrooms in Mathematics” PDF, directly supports the eight Standards for Mathematical Practice. The emphasis on problem-solving, reasoning, and argumentation aligns perfectly with these standards.
Students are consistently engaged in constructing viable arguments, critiquing the reasoning of others, and modeling with mathematics through the use of vertical non-permanent surfaces and collaborative tasks. This approach moves beyond rote memorization, fostering a deeper, more conceptual understanding of mathematical principles and promoting genuine mathematical proficiency.
Resources and Further Exploration
For educators seeking to implement Building Thinking Classrooms, the core text, “Building Thinking Classrooms in Mathematics” PDF, is an essential starting point. Supplemental materials, like “Modifying Your Thinking Classroom for Different Settings,” offer practical adaptations.
Online resources include videos from the 2023 Virtual Math Summit featuring Peter Liljedahl, and information from DoDEA’s professional development initiatives. Exploring these resources will provide a comprehensive understanding of the methodology and support successful implementation in diverse educational contexts, fostering a shift towards student-centered learning.
Impact on Student Learning and Achievement
Implementing Building Thinking Classrooms, guided by resources like the “Building Thinking Classrooms in Mathematics” PDF, demonstrably impacts student learning. The focus on thinking, rather than rote memorization, cultivates deeper understanding and problem-solving skills.
This approach addresses math anxiety, building confidence and fostering a more positive attitude towards mathematics. Professional development programs, such as those by DoDEA and the Mississippi State partnership, suggest improved student engagement and achievement through these innovative pedagogical shifts, ultimately leading to more successful mathematical outcomes.
Future Trends in Thinking Classroom Implementation
The future of Building Thinking Classrooms, informed by resources like the “Building Thinking Classrooms in Mathematics” PDF, points towards wider adaptation and refinement. Expect increased integration of digital tools to support Vertical Non-Permanent Surfaces and collaborative learning.
Further research will likely focus on tailoring implementation to diverse student populations and subject areas beyond mathematics. Continued professional development, mirroring DoDEA’s and Mississippi State’s initiatives, will be crucial. The trend suggests a move towards more student-centered, thinking-focused classrooms, prioritizing conceptual understanding over procedural fluency.
